推 there801021:一直想說是2S分之ㄧ 結果是二分之ㄧS 難怪算不出來.. 09/19 12:17
推 b7616734:good~ 09/20 13:14
※ 引述《irradiance (nofeeling)》之銘言：
: 1.年級：國中二年級
: 2.科目：理化
: 3.章節：直線運動
: 4.題目：某物體初始速度為3 m/s，做等加速度運動前進，經一段時間後末速度為21 m/s，
: 總路徑長為S，試問當物體在1/2S位置時其速度為何？
: 5.想法：1.設在1/2S位置時速度為X m/s
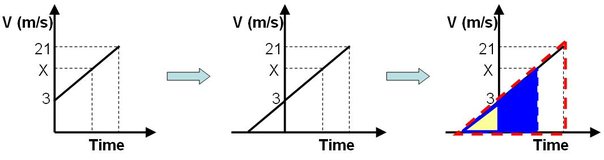
: 2.先畫出V-t圖 → 將線段延長 → 可看到三個相似三角形
: 面積由小至大標為△1、△2、△3
: (邊長比為3:X:21，面積比為9:X^2:441)
: http://images.plurk.com/3289575_76504a3fd1dfcab7608464ee1831e61b.jpg
: 3.△3 - △2 = △2 -△1
: △3 + △1 = 2△2 --------(1)
: 4.△1:△2:△3 = 3^2: X^2 :21^2
: 可得△1 = (3/X)^2˙△2
: △3 = (21/X)^2˙△2
: 將此結果帶入(1)
: 5.[(9 + 441)/X^2]˙△2 = 2△2
: 225 = X^2
: X = 15
: 想請教各位是否有更快速的算法？
面積比△1:△3 = 1k:49k
所以△3-△1的梯形面積應為49k-1k= 48k, △2-△1題目說是一半 也就是24k
所以 面積比 △1:△2=1:(1+24)=1:25
邊長比為1:5 =3:15
得速度是15
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.24.198.140