[閒聊] 理科生的廁所花子

[knight45683 (今晚去吃烤肉)]

https://x.com/man_Arihred/status/1732342140620116346?s=20
https://pbs.twimg.com/media/GAqD2yTacAAqaoZ.jpg

【晚上的學校三樓】

「來觀察蟲子的不小心看到這麼晚了」
「上個廁所就回去吧...」

【明明空無一人的女生廁所】

【在第O間的門內】

https://pbs.twimg.com/media/GAqECbTaYAAdI-1.jpg

【有理組的花子在】

【似乎看到了就會被帶去那邊的世界】

https://pbs.twimg.com/media/GAqEC4PaEAAmo4V.jpg

「怎...怎麼辦 如果真的有花子在的話...」
「確實是在三樓的女廁...但第幾扇門...忘了...」
「如果不小心開到的話......」

「機率是三分之一嗎...」

(我要冷靜點...怎麼可能有花子在啊...)

(準備打開第二扇門)

https://pbs.twimg.com/media/GAqED0gaoAEDuxi.jpg

(第一扇門突然發出聲響)

「門是鎖起來的...旁邊有誰在嗎...？」

(改去第一扇門)

「...花子...請問妳在嗎...？」

https://pbs.twimg.com/media/GAqEEbRbUAAPUF0.jpg

「 在 」
(！？)

(不在這扇門內...聲音是從左邊傳來的...)
(但到底是第二間還是第三間.....)

「怎麼辦...變二分之一了...)

「有一間裡有花子...如果打開的話...」

https://pbs.twimg.com/media/GAqEKRcaMAAk1u3.jpg

「不對...不是二分之一 這是...蒙提霍爾問題！」

蒙提霍爾問題(山羊問題、三門問題)


少女選了其中一扇門
接著花子把自己不在的剩下那間門給鎖起來
接著重選 門裡有花子在的機率乍一看是二分之一

https://pbs.twimg.com/media/GAqEKtjacAA-eo4.jpg

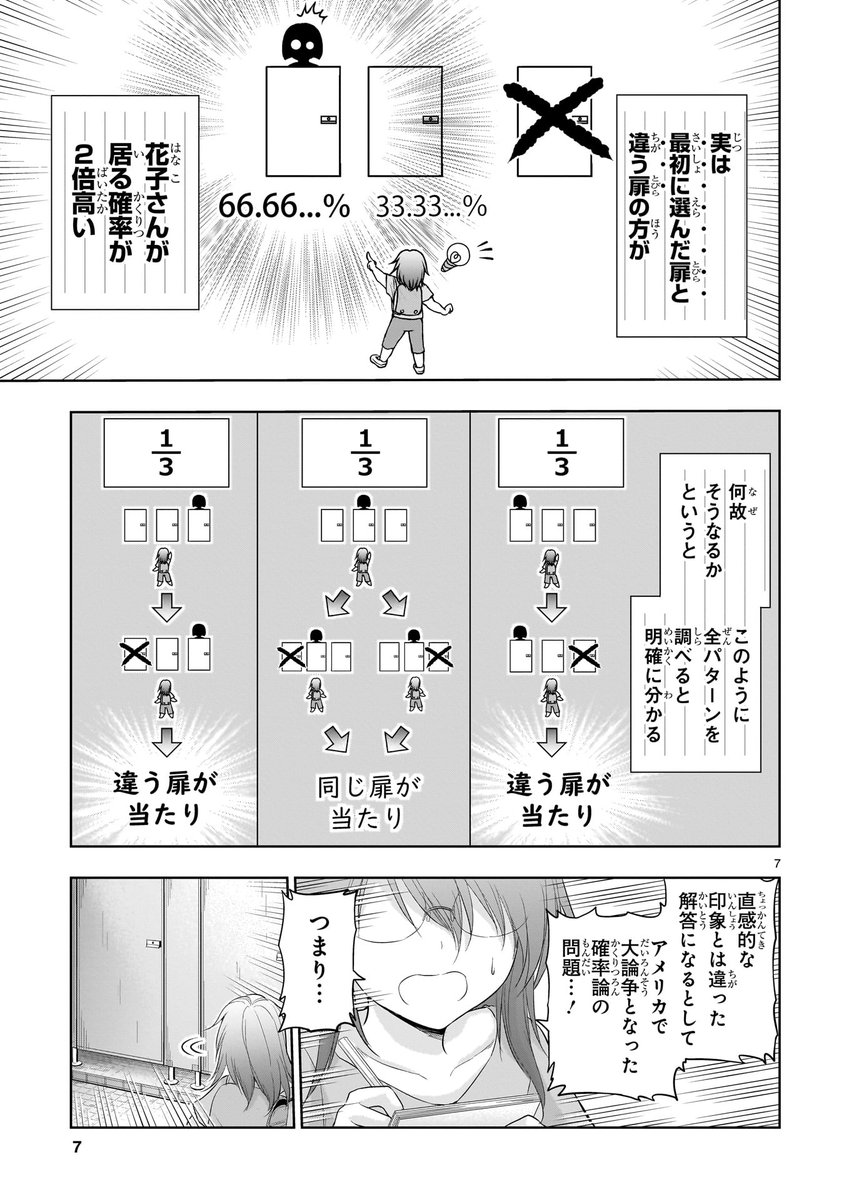
但其實不然 其實選跟最開始那扇不同的門
裡面有花子的機率竟有兩倍之高

為什麼呢
像這樣把全部的路線畫出來就很明瞭了

「這是答案很反直覺 在美國也引起廣大爭論的機率問題...！」
「所以說...！」

https://pbs.twimg.com/media/GAqELGqbIAAJWMl.jpg

「花子在第三間裡面！」

「果然沒錯~！這是蒙提霍爾問題的重現對吧」

「能明白這個梗的人妳還是第一個呢...」

「果然是呢~！」

https://pbs.twimg.com/media/GAqELmebwAA1rjN.jpg

然後少女跟花子
兩人因興趣相投 互相理解了

「這題真有趣呢 妳也喜歡數學嗎？」
「嗯...接著來討論柯尼斯堡七橋問題吧」
「來吧來吧」

就這樣 兩人不斷的討論直到三更半夜——



「...以前 好像有過這樣的事 但那是現實嗎 還是夢呢...」

(現實才不可能那種事發生吧)


.
.
.


看到三選一

腦袋就浮現了三門問題 也是很經典的題目呢

想起來以前大學在補習班打工的時候

看到國中生的考卷竟然出了這題還讓我驚訝了一下

是說這題第一次見的話

國中國小根本寫不出來吧

太反直覺了


--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 27.242.30.30 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/C_Chat/M.1701926110.A.94F.html
推 kirimaru73: 考試時間夠有筆的話，就是樹狀圖開下去
推 kaj1983: 長大後也變得太多了吧...
推 w60904max: 碰到這類問題就放大規模來看 1000個門鎖上998個
推 undeadsin: 花子還拿數學課本www
推 tonyxfg: 不過選對的機率只有三分之二，在只有一次選擇機會下其實
→ tonyxfg: 還是很可能失敗的XD
推 GaoLinHua: 太可怕了 是三門問題
推 qwe04687: 笑死
推 heybro: 這世界的鬼怪都特別好學，之前那個筆仙也很扯XD
推 joy82926: 這花子是理科的呢
→ joy82926: 裂嘴女那個好像就普通被撩而已?
推 Issarc0721: 有梗XD
推 Hazelburn: 看了這篇才知道 超神奇 很違反直覺
推 sectionnine: 筆仙是被強迫的吧XDDD
推 Gokudo: 畢竟學力等同戰鬥力的世界觀 需要吧w
推 kirimaru73: 花子在左邊：她只能鎖最右邊的門，100%符合實際條件
→ kirimaru73: 花子在中間：她可以鎖左或右邊的門，50%符合實際條件
→ kirimaru73: 所以花子在左邊的機率是在中間的兩倍
→ kirimaru73: 這是不畫圖時比較勉強能解釋的一種說法，但還是很抽象
推 SOSxSSS: 簡單來說只有一開始就選中1/3的花子才能換門避開，2/3共
→ SOSxSSS: 菇的你換門就是遇到花子
推 hayate1143: 筆仙救我高微
推 kirimaru73: 可以請筆仙計算Σ(-1)^n的級數極限是多少
→ kirimaru73: 然後就可以發明簡易版的永動機
推 jeff235711: 拜託給我修女
推 xji6xu4yjo41: 喔 貝氏統計
推 YaLingYin: 三門問題 我記得八卦版有一篇討論超長
推 wison4451: http://i.imgur.com/NjEauG7.jpg
推 Electricfish: 那個花子也太獵奇......
推 AfterDark: 花子：聊到忘記賺業績了 失敗
推 hongjachun: 笑死XD
推 jackeo: 聊著聊著都能順便超渡了吧
推 jeff666: XDDD
推 Haruna1998: 是什麼21點電影裡面那個嗎？
推 tiger870316: 花子跟筆仙強強聯手 人類科技應該可以快進一百年
推 Qorqios: wwwwwwwwww