Re: [閒聊] 每日LeetCode

[ZooseWu (動物園 公告)]

935. Knight Dialer

西洋棋的騎士只能往前兩步後往左或右走一步

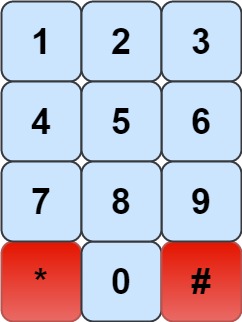
有一個撥號板如下圖
https://assets.leetcode.com/uploads/2020/08/18/phone.jpg

騎士只能站在數字上(藍色按鈕)

回傳騎士在撥號板上能走的所有可能的數量mod 10^9+7


Input: n = 1 Output: 10
每一格都可以踩 共十種


Input: n = 2 Output: 20
所有可以走的路徑是
[04, 06, 16, 18, 27, 29, 34, 38, 40, 43,
49, 60, 61, 67, 72, 76, 81, 83, 92, 94]


Intuition:

之前好像也有遇到一題類似的題目

思路是把能走的路徑反轉思考成這格能從哪邊來

紀錄可能走到這一格的可能數並不斷重複計算就好


Approach:

先定義所有可能走到此格的陣列 stepRefs

例如 stepRefs[0] = [4, 6]

代表號碼4跟號碼6可以走到號碼0

所以我們把號碼4的數量跟號碼6的數量加起來

就是號碼0下一步可能的所有數量



這一次我開始用FP去實現演算法

雖然速度稍微變慢了一點

但是可讀性up up


不過還有可以改進的地方

現在會把資料傳進去

要想辦法改成只關注方法

另外之後還得自己實作compose跟curry



下面兩種版本都放上去

TS Code with FP:

const mod = 1000000007

const stepRefs = [
  [4, 6], [6, 8], [7, 9], [4, 8], [3, 9, 0],
  [], [1, 7, 0], [2, 6], [1, 3], [2, 4],
]

function calculateNextStepElement (refIndexes: number[], prevArray:
number[]): number {
  return refIndexes.reduce((result, index) => result + prevArray[index], 0)
}

function calculateNextStepArray (prevArray: number[]): number[] {
  return stepRefs.map(stepRef => calculateNextStepElement(stepRef, prevArray)
% mod)
}

function calculate (n: number, arr: number[]): number[] {
  return n === 1 ? arr : calculate(n - 1, calculateNextStepArray(arr))
}

function knightDialer (n: number): number {
  return calculate(n, new Array(10).fill(1))
    .reduce((result, currValue) => result + currValue) % mod
}


TS Code:

const mod = 1000000007

const stepRefs = [
  [4, 6], [6, 8], [7, 9], [4, 8], [3, 9, 0],
  [], [1, 7, 0], [2, 6], [1, 3], [2, 4],
]

function knightDialer (n: number): number {
  let currentStepArray = new Array(10).fill(1)

  const calculateNextStepElement = (refIndexes: number[]): number => {
    let nextStep = 0
    for (let i = 0; i < refIndexes.length; i++) {
      nextStep += currentStepArray[refIndexes[i]]
    }
    return nextStep
  }

  for (let i = 1; i < n; i++) {
    const newArray: number[] = new Array(10)
    for (let i = 0; i < currentStepArray.length; i++) {
      newArray[i] = calculateNextStepElement(stepRefs[i]) % mod
    }
    currentStepArray = newArray
  }

  let result = 0
  for (let i = 0; i < currentStepArray.length; i++) {
    result += currentStepArray[i]
  }

  return result % mod
}

--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.32.229.33 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1701059517.A.264.html
推 SecondRun: FP好玩
推 wwndbk: 大師
→ ZooseWu: FP真的蠻讚的 不過不知道C#寫FP的時候會不會有GC的問題
推 sustainer123: 大師 今天好難 哭了
這題的思路跟 #1bFA7kJT (Marginalman) 一樣

你寫完這一題可以去試試看前面那題

或是這一題卡住了先試試看前一題


我現在在補昨天的

我反而覺得昨天超難

完全沒有想法
※ 編輯: ZooseWu (114.32.229.33 臺灣), 11/27/2023 13:00:09