→ Firstshadow: 大師 06/30 01:10
推 ririoshi: 大師 06/30 01:14
推 ILoveErr: 大師 06/30 01:14
https://leetcode.com/problems/path-with-maximum-probability/description/
1514. Path with Maximum Probability
給你一個大小為 n 的無向圖資訊，陣列 edges[] 表示邊關係，succProb[] 表示邊的機
率權重，路徑經過時需要乘以該權重，求出從 start 走到 end 的路徑，他的最終權重必
需是最高，走不到則返回0。
Example 1:
https://assets.leetcode.com/uploads/2019/09/20/1558_ex1.png
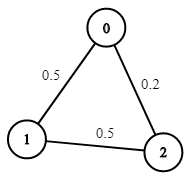
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start =
0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability
of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
https://assets.leetcode.com/uploads/2019/09/20/1558_ex2.png
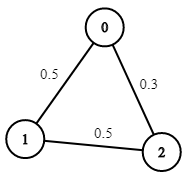
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start =
0, end = 2
Output: 0.30000
Example 3:
https://assets.leetcode.com/uploads/2019/09/20/1558_ex3.png
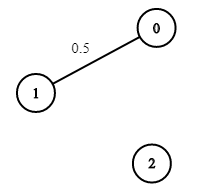
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.
思路：
1.圖形的最短路徑問題要先想到 BFS，但是因為每個邊的權重不同所以不能用 Queue 去
做，第一個到達終點的未必是最短路徑，所以我們改用 maxHeap 來讓每次都從機率最
大的路徑開始計算。
2.然後額外加入一個表紀錄之前算過的每個點的最大機率，只有新的機率使舊的變高才
更新。
3.如果最後到達不了 end 就返回 false。
Java Code：
-------------------------------------------------------
class Solution {
public double maxProbability(int n, int[][] edges, double[] succProb, int
start, int end) {
List<double[]>[] graph = new ArrayList[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < edges.length; i++) {
int[] edge = edges[i];
int v = edge[0];
int u = edge[1];
double p = succProb[i];
graph[v].add(new double[] {(double) u, p});
graph[u].add(new double[] {(double) v, p});
}
PriorityQueue<double[]> maxHeap = new PriorityQueue<>(
Comparator.comparingDouble(d -> -d[1]));
maxHeap.offer(new double[] {start, 1.0});
double[] rate = new double[n];
Arrays.fill(rate, -1);
while (!maxHeap.isEmpty()) {
double[] curr = maxHeap.poll();
int currId = (int) curr[0];
double currRate = curr[1];
if (currId == end) {
return currRate;
}
if (currId != start && currRate < rate[currId]) {
continue;
}
for (double[] next : graph[currId]) {
int nextId = (int) next[0];
double nextRate = next[1] * currRate;
if (nextRate > rate[nextId]) {
rate[nextId] = nextRate;
maxHeap.offer(new double[] {(double) nextId, nextRate});
}
}
}
return 0;
}
}
-------------------------------------------------------
晚安
--
https://i.imgur.com/tdaniED.jpg
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 122.100.75.86 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1688058500.A.805.html