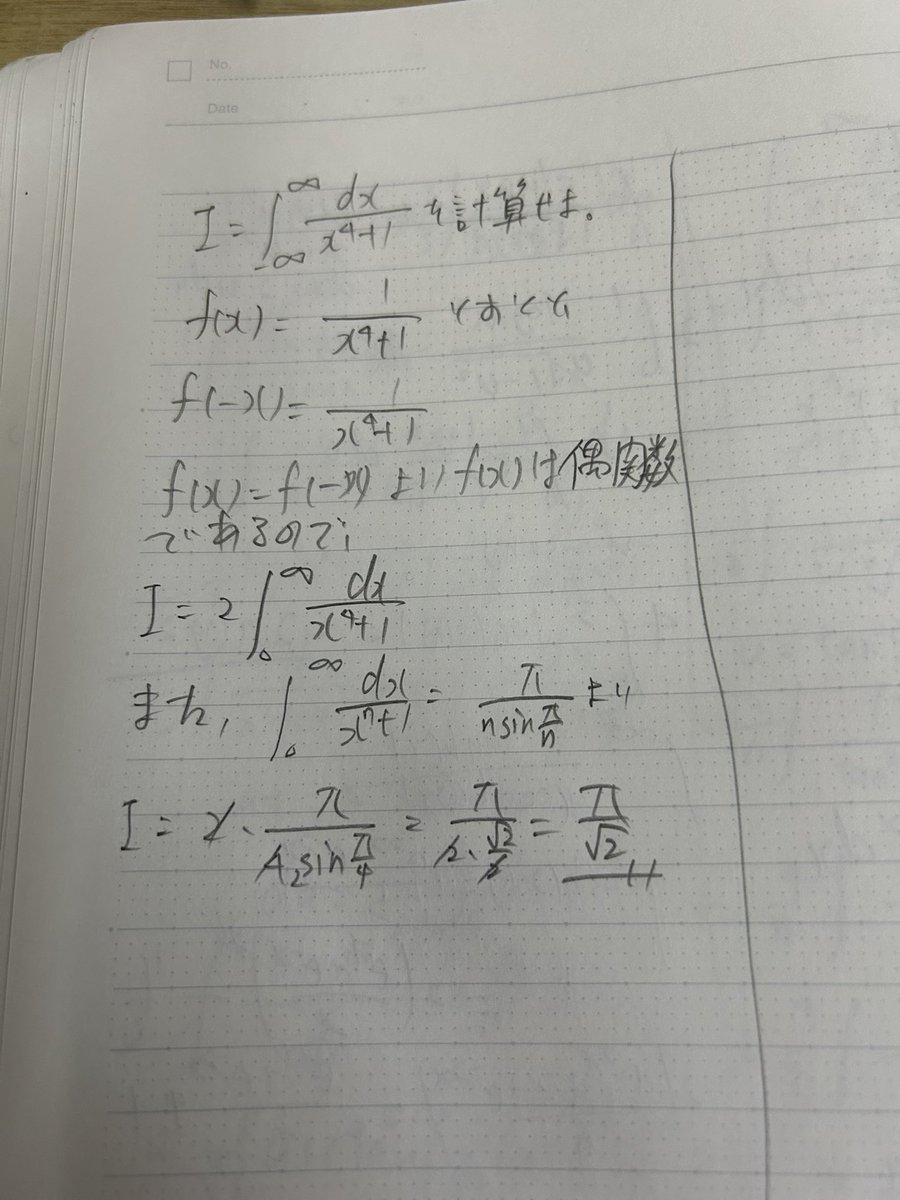Re: [蔚藍] 伊吹：老師你看 考了100分

[nahsnib (悟)]

※ 引述《dahos (dahos)》之銘言：
: https://x.com/lam/status/1911615402217553983
: https://pbs.twimg.com/media/Godro06WUAAFqJ5.jpg
: 題目
: 請計算
: https://i.imgur.com/4G1FQwj.jpeg
: 算式
: https://i.imgur.com/G4namvH.jpeg
: 推特上有其他人驗算是對的
: https://x.com/XGn7ogANxW41985/status/1911769614817833185
: https://pbs.twimg.com/media/Gof4U0wWAAAjdHv.jpg
: https://x.com/tatikaze_miyako/status/1909872250817593810
: https://pbs.twimg.com/media/GoE6sL_aUAAplj9.jpg
: ---------------------
: https://i.imgur.com/mg1Ym9A.gif


大家一起來跟著好孩子伊吹學數學吧！

首先，要知道，「所有有理函數都有反導函數」！（總之就是可以不定積分）

有理函數包含所有可以表示為兩個多項式相除的函數，例如x/(x-1)包含在內。

所以本題中的1/(1+x^4)當然也有反導函數，這麼說來不就很簡單了嘛！

所以方法一：找優香幫忙因式分解。

1/(1+x^4) = i/2 * [ 1/(x^2 +i) - 1/(x^2 -i) ]

我甚至還沒有因式分解到最後一步，這條路線顯然不可行。

順帶一提做到底的結果將會需要處理類似ln(i)這種看到就會頭痛的數字。

...雖然，其實也不是不能做啦，將i用棣美弗定理表示為e^(i*pi/2)，

取自然對數便會得到i*pi/2的結果就是了


方法一徹底失敗，U卡媽媽可以先回去了，你說什麼？抱歉那隻蘿莉是萬魔殿團寵，

請不要對她動歪腦筋。


方法二：冪級數

眾所皆知的，1+1/2+1/4+... = 1 / (1- 1/2)，

那麼我們能不能把這個操作反過來做？

當然可以，於是我們就有：1 / (1 - x ) = 1 + x + x^2 + x^3 + ...

同樣的道理套用到原題目，就得到

1 / [ 1 - (- x^4) ] = 1 - x^4 + x^8 - x^12 + ....

這東西當然是可以積分的！

對其積分得到 x - x^5 / 5 + x^9 / 9 - x^13 / 13 +...

所以這是啥？

......呃，方法二失敗！


事實上你去找積分表也會發現積分表沒有寫到這邊，光是使用初等微積分與工程數學

的內容根本無法解決這道題目，這樣大家對於十一歲的伊吹有沒有肅然起敬了呢？


那怎麼做？俗話說的好，平面上的問題無法解決時，有時候在三維空間就能秒殺。

而這題也類似的，當我們要對整條x軸做積分，不如我們將範圍擴張一下吧？

這裡的擴張並不單純只是向y軸擴張，我們是要對虛軸擴張。

https://imgur.com/SRtdfmF

想像這樣一個虛數平面上的半圓形，沿著半圓形逆時針走，會得到什麼呢？

你會得到一個是0但是又不是0的東西。

工三小？？

事情是這樣的，封閉路徑上的積分應該要是0才對（柯西積分定理），

但是如果這個曲線包住了一些討厭的東西，那就會導致不好的後果，

我們得把這些壞胚子吊起來，就如同我們對待那些殘黨。

沒錯，這就是複變函數論中所說的留數定理，又稱殘數定理。



那又跟我們的原題目有啥關聯？

回想一下剛才那個半圓形，如果我們把半徑推到無窮大，

那麼底下的直線部分就是我們想要的積分範圍。

上半圓呢，也不用擔心，反正半徑無限大的時候他會是0的。

所以簡單來說是這樣的：

沿著整個半圓積分 = 殘黨

        ||

沿著半圓積分 + 沿著直徑積分

        ||（半徑推到無窮之後）

 0 + 我們想算的東西

所以原題目就是那些殘黨！


首先我們得找出那些殘黨，殘黨就是一群會讓分母為0的兔崽子，

好消息是，這些殘黨剛好在我們的方法一算過了，感謝U卡媽媽！

他們剛好是e^(i k pi/4)，k = 1, 3, 5, or 7

完美，只有兩個位於我們想積分的範圍內，所以最後就知道你想算的東西可以表達為

那兩點的留數，

pi/2i * [ e^(i pi/4) + e^(3i pi/4)] = pi/2i * [i sqrt2] = pi / sqrt2


真是令人讚嘆不已！All Hail Ibuki! All Hail IBUKI!




--
以雙眼親睹靈魂的奧秘
以雙手掌握生命的法則

人類不應觸及，僅屬於神祇的禁忌之天頂…不曾存在！

--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.161.100.145 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/C_Chat/M.1745019401.A.3D7.html
推 brightriver: 雖然個人數學不好不太懂，但是行文很有趣，推推
推 qsx889: 恩恩 還是來吃布丁
推 nakasorachi: 推
推 bautz: 嗯嗯 跟我想的一樣
推 jamiexgw: 謝謝伊吹 我會了
※ 編輯: nahsnib (114.137.151.56 臺灣), 04/19/2025 08:25:08
推 XD9527XD: 對對 跟我想的一模一樣
推 castawil: 謝謝你一大早就讓我覺得自己蠢的跟小春一樣
沒關係，我們也跟小春一樣色，所以大家都是小春！
推 sarspieya521: 我是誰？我在哪？我在做什麼？
推 smallreader: 數學小老師
推 Heisenberg29: 已經完全看不懂了...
→ spfy: 你竟然想試圖教會我?
大家一起跟伊吹一起預習複習吧
推 GatanGoton: 對的 就是這樣，跟我算的一樣
推 qlz: 於是你告訴我我的微積分基本上已經還給老師了.......
教育現場常有的一句話：你要還給老師，那你要先從老師那裏得到過啊
推 inte629l: 伊吹妳複變有點猛阿...只記得和柯西主值有關，而且積分
→ inte629l: 好像要上半平面有限個poles還啥的，超級妙的
複變真美好，實變狗屎
推 apulu0507: .….？
推 schula: 好強，但看完突然睡意，襲來！
不瞞你說我也是邊打邊睡
推 wl00533180: 跟我想的一樣
※ 編輯: nahsnib (1.161.100.145 臺灣), 04/19/2025 09:17:16
推 OrangeTissue: 懂了 其實我根本就是小春 身上已經長蝦線出來了
→ kimokimocom: 整篇全是中文 聚在一起就..
→ fgh81113: 對對 我也是這樣想的
推 mark0912n: 老師老師，我有問題，上面日本推特網友的計算，到偶函
→ mark0912n: 數拆兩半都看得懂
→ mark0912n: 但是那個積分結果怎麼來的
他開了緋紅之王，繞過所有留數定理的過程，只保留結論的算式！
對基本上就是他的積分表比較大一張啦

推 DivineSX: 整篇看完我只懂一句話All Hail Ibuki! All Hail IBUKI!
※ 編輯: nahsnib (1.161.100.145 臺灣), 04/19/2025 09:58:35
推 lsd25968: 請數學O放過西洽（x
推 mark0912n: 了解了
噓 coon182: ID錯誤
→ Innofance: 我來C恰不是看這個的==
推 denny8437: 數學老師
推 qlz: 好歹當年微積分學分有拿到, 所以算曾經得到過吧(逃)
推 AkikaCat: 跟我想的一樣
→ tomalex: (′・ω・‵) 這裡不是數學版==
推 jasonx105: 嗯跟我算得一樣（完全沒懂
推 mystina43: 留數定理的知識早就消失不見了
推 mumiko5566: 懂了 是那個修完在腦袋沒留下任何東西的複變
推 Alexander1: 伊吹留下來給我家教一下好不好
→ Dlareme: 我還是左轉去看瑟圖就好
推 kirimaru73: 以這個課程來說這題算基本題，伊吹有學的話會解不奇怪
→ kirimaru73: 不過我很肯定我沒有學，資訊工程系必修沒有這個
推 DecadeCay: 資工有基礎微積分+離散+線代+機率統計就夠了 工數不是
→ DecadeCay: 必修 雖然我校是必修
推 jeff666: 推