→ wayne2011 : 因為0 < alpha < pi ,所以alpha=角CDB=pi/6,故得證. 12/05 20:52
※ 編輯: wayne2011 (61.58.103.35), 12/05/2018 20:52:32
→ wayne2011 : 希望可以講到大家可以當"老師"的程度~我就非常happy 12/05 21:39
※ 引述《ccccc7784 (龍王號)》之銘言：
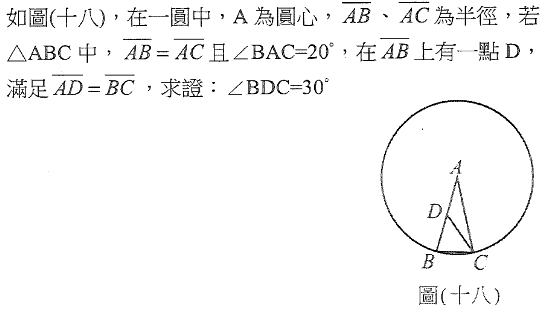
: 如圖
: https://upload.cc/i1/2018/12/04/cHLsB7.png
: 請問應該如何下手?
: 先謝謝各位老師
假設
角CDB=alpha,(c-a)/sin[(5pi/9)-alpha)]=a/sin(alpha)
[sin(4pi/9)/sin(pi/9)]-1=sin[(4pi/9)+alpha]/sin(alpha)
sin[(4pi/9)+alpha]=sin(alpha)[4cos(pi/9)cos(2pi/9)-1]
sin(4pi/9)cos(alpha)=sin(alpha)[4cos(pi/9)cos(2pi/9)-cos(4pi/9)-1]
cot(alpha)=[1/sin(pi/9)]-cot(4pi/9)-[1/sin(4pi/9)]
=[1/sin(pi/9)]-[1+cos(4pi/9)/sin(4pi/9)]=[1/sin(pi/9)]-cot(2pi/9)
=[2sin(7pi/18)-cos(2pi/9)]/sin(2pi/9)
={2sin[(pi/6)+(2pi/9)]-cos(2pi/9)}/sin(2pi/9)
=[cos(2pi/9)+(sqrt3)sin(2pi/9)-cos(2pi/9)]/sin(2pi/9)=sqrt3
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.58.103.35
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1544010251.A.7D3.html
※ 編輯: wayne2011 (61.58.103.35), 12/05/2018 20:44:11