連到 https://csacademy.com/app/graph_editor/
將一個個畢氏三角填進入：
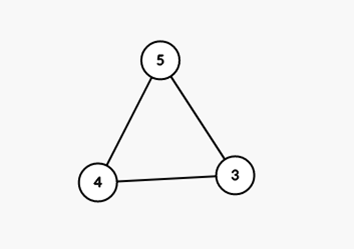
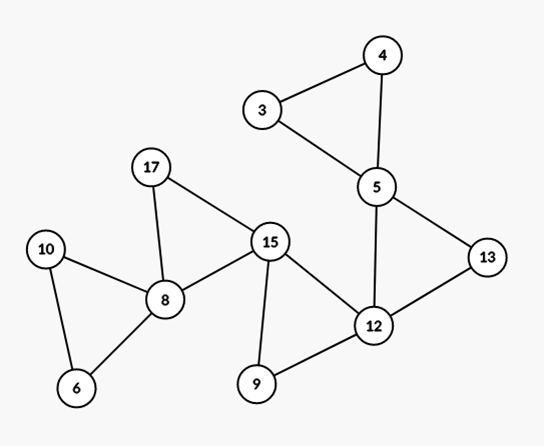
第一個是經典的(3,4,5)
https://i.imge.tw/uVh.png
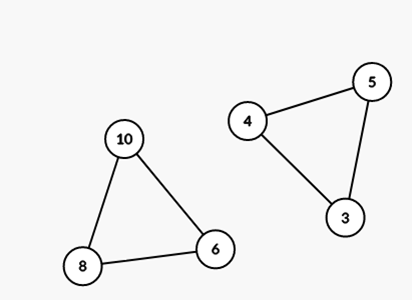
(6,8,10)，不求互質的話是第二小的畢氏三角
https://i.imge.tw/uV3.png
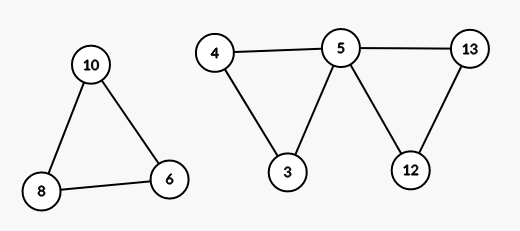
(5,12,13)，國中生通常就是背3,4,5跟這個
https://i.imge.tw/uVO.png
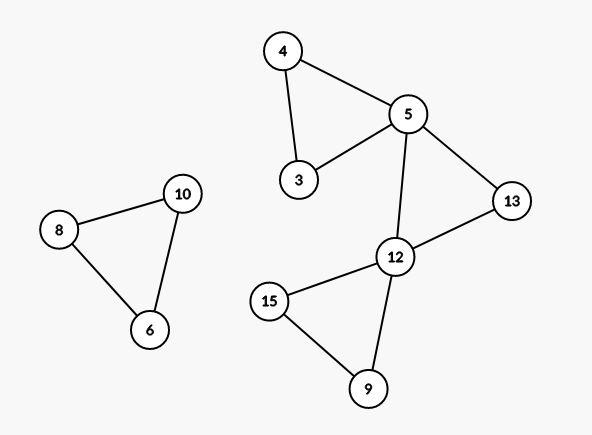
(9,12,15)
https://i.imge.tw/uVC.png
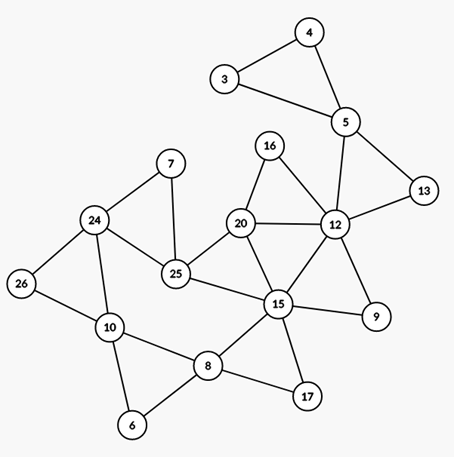
(8,15,17)，此時形成連通圖
https://i.imge.tw/uVu.png
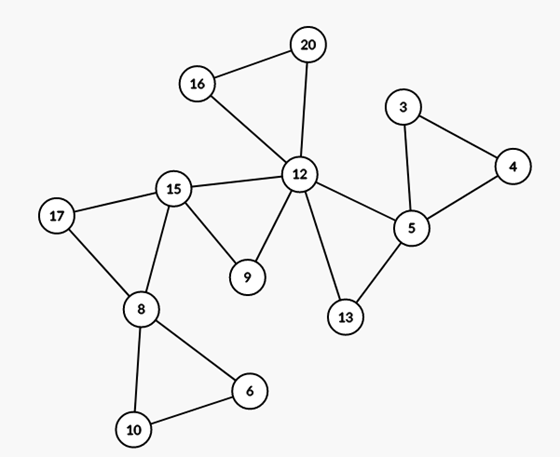
(12,16,20)
https://i.imge.tw/uVW.png
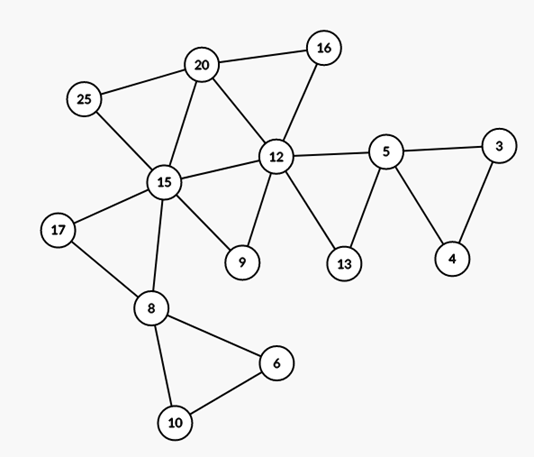
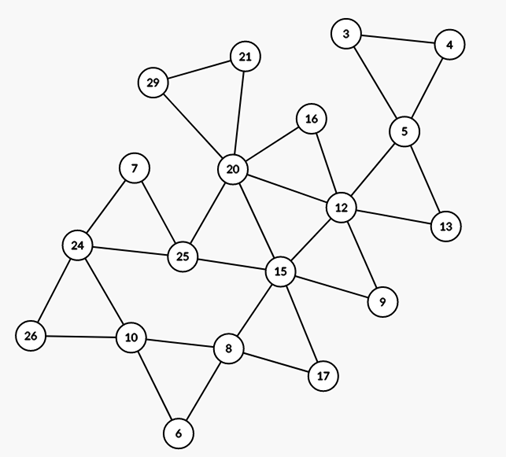
(15,20,25)
https://i.imge.tw/uVG.png
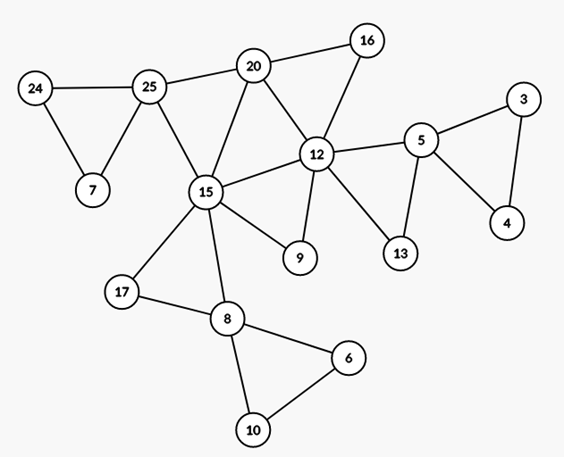
(7,24,25)，結構還算漂亮
https://i.imge.tw/uVt.png
(10,24,26)，開始有非三角的迴路出現
https://i.imge.tw/uVs.png
(20,21,29)，也就是圖形開始變「醜」了
https://i.imge.tw/uVS.png
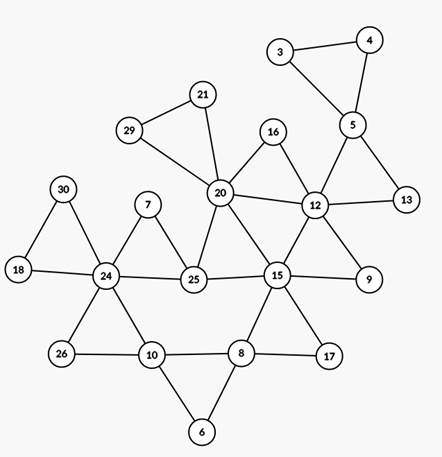
(18,24,30)，開始需要手動拉成平面圖
https://i.imge.tw/uVd.png
(16,30,34)，線條也曲化不是直線
https://i.imge.tw/uVj.png
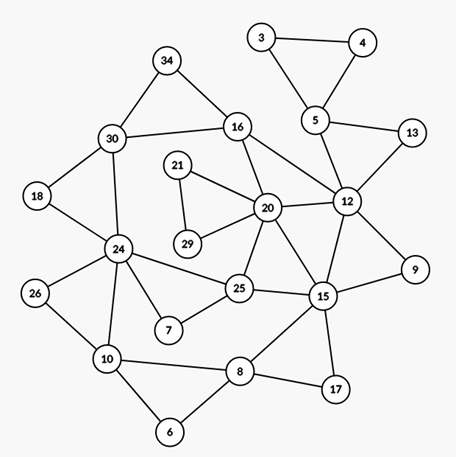
(21,28,35)，要手動拉的時間越來越久
https://i.imge.tw/uVc.png
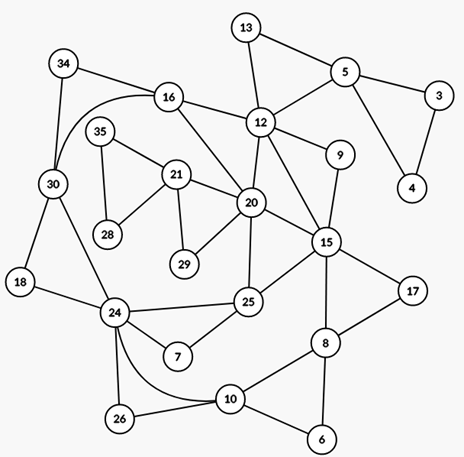
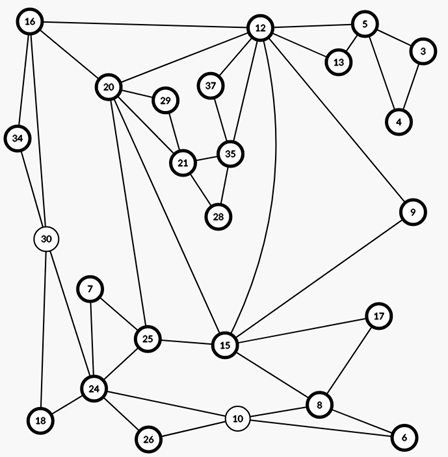
(12,35,37)，不想繼續拉不下去的臨界點...
https://i.imge.tw/uV6.png
讓我好奇的是
如果繼續下去
是否可以一直維持著平面圖的特性？
https://zh.wikipedia.org/wiki/%E5%B9%B3%E9%9D%A2%E5%9B%BE_(%E5%9B%BE%E8%AE%BA)
還是會成為非平面圖呢？
非平面圖一定包含K5或是K3,3
K5想想不可能
等於存在五個數字，任取三個都可以形成直角三角形，共十種組合！
假設五個數字為 a < b < c < d < e
那麼(a,b,c)的直角三角形一定是 a^2 + b^2 = c^2
(a,b,d)的直角三角形也一定是 a^2 + b^2 = d^2
矛盾了這個
K3,3的話比較複雜
想不透要如何舉出實例或是證明不存在
目前看每個數字degree最大都是6
但是隨著數字增加，degree應該會有大於6的...
從畢氏三元數來看
a = m^2 - n^2
b = 2 m n
c = m^2 + n^2
目前看到有6個degree的點
分別代表了三種三角形的a與b與c
但不代表a與b與c只能被代表一次
只要數字夠大，質因數夠多，就可以有多組的m,n湊成a或b或c
比如
180 = 46^2 - 44^2 = 18^2 - 12^2 = 14^2 - 4^2
180 = 2 45 2 = 2 30 3 = 2 18 5 = 2 15 6
......應該寫個程式去算的
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 60.251.148.94 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1719457758.A.1BF.html