→ buffalobill : 進展大概是這張圖最右邊的黑線再往右40px左右 10/22 10:08
https://www.mersenne.org/primes/?press=M136279841
M136279841 共計 41024320 位數
Matt Parker 就連在渡假中都擠出時間來拍了片速報:
https://www.youtube.com/watch?v=zsyGRDrDfbI
中間將近六分鐘的時間是用 25 fps 的影片每影格 4000 個數字來顯示這個質數 XD
(這個速度每秒會閃過十萬位數, 所以全部四千一百多萬位要約 410 秒將近六分鐘)
這個質數的發現還標誌了兩個梅森質數搜尋計畫的變革:
其一是 GPU 的應用, 早在 2017 已經有志願者將搜尋程式寫成 GPU 版本的, 叫 GpuOwl
https://github.com/preda/gpuowl
而發現這個質數的 Luke Durant 他是前 NVIDIA 員工
他使用了分布在 17 個國家, 24 個資料中心的 GPU 的計算網路參與計算
在參加約一年之後找到了這個質數
GPU 的參戰效果體現在找到的這個質數的大小:
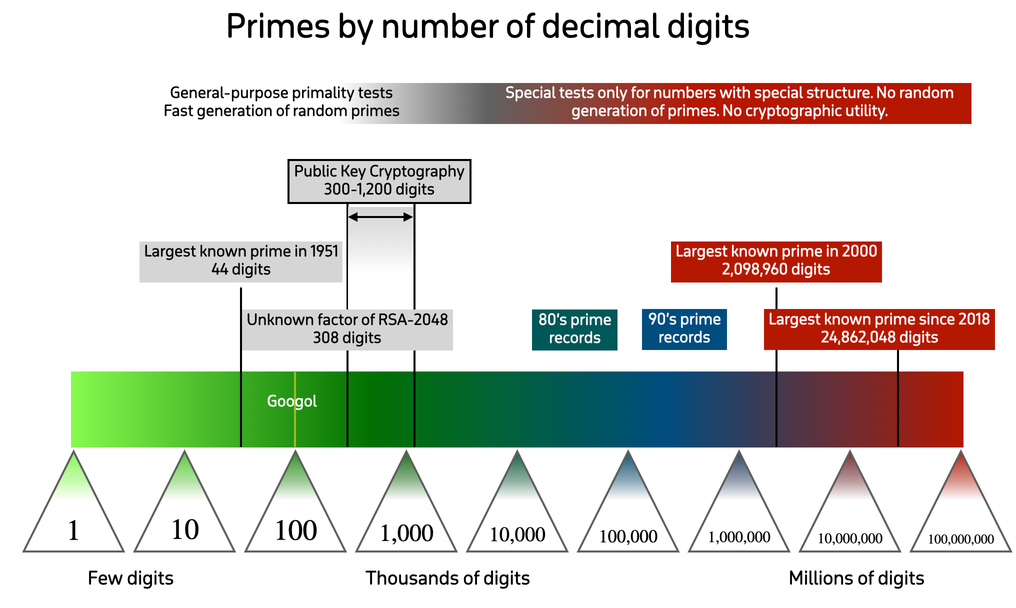
前紀錄是六年前的 M82589933 共 24862048 位
在這之前的位數推進速度大概是每年一兩百萬位左右
這次的紀錄位數在這六年間一口氣多了一千六百多萬位
另一是搜尋方式的改變
八年前發現 M74207281 時版上有文章 (#1MecIDJV (Math))
介紹了梅森質數的判別演算法 Lucas-Lehmer
不過後來根據一些結果發現, 如果能先用一些機率性可能質數檢驗法粗篩的話
可以不用每個梅森數都去跑這個演算法
他們選的粗篩演算法是大家熟知的費馬小定理的逆敘述:
若 (a,p) 互質, a^(p-1) 除以 p 餘 1 對某個或某些 a 成立, 則 p 很有可能是質數
但如果有一個 a^(p-1) 除以 p 不餘 1 則 a 一定不是質數
之所以可以用這個粗篩快速篩選的原因是, 我們在找的質數是 2 的次方減 1
a^(p+1) 會是 a 的"某個 2 的次方數"次方, 可以由 a 開始連續平方而得
這個計算速度會比起完整的 L-L 來得快 (因為 L-L 除了平方還有 -2)
今天這個質數就是第一個先用粗篩篩出來之後再用 L-L 檢驗一次確認的
考慮到 L-L 檢驗的參數, 這裡的粗篩實作 (PRPLL 程式) 選用了 a=3 做為判斷條件
有趣的是, 這兩個檢查都是 Luke Durant 的雲端 GPU 網路中的機器做的:
粗篩是他在愛爾蘭的都柏林的 NVIDIA A100, 在 10/11 進行的
實際檢驗則是他在美國德州聖安東尼奧的 NVIDIA H100, 在 10/12 進行的
這個質數的正式發現日則是被定在正式 L-L 檢驗證實的那一天 (10/12)
隨後在其他志願者的機器獨立檢驗確認之後在今天正式公布
--
將很小又單純的命令《Code》組合成函數《Function》。函數累積成更大更方便的元件《
Parts》，成為程式《App》。接著進行動態結合，相互通訊，打造出服務《Service》。
李奧納多知道，要得到結果，就必須持續進行非常單純的作業。為了展現出匹敵巨大建築
的技術，現在非得將面前的碎片組合起來。
知道這條路多麼遙遠的人，叫做極客《Geek》。
將這份尊貴具體呈現的人，叫做駭客《Hacker》。 －－記錄的地平線 Vol.9 p.299
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.194.181.180 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1729530793.A.9AB.html