推 Rimowa : 受教了 11/21 18:39
※ 引述《Rimowa (德國品質)》之銘言：
: 親戚小孩問我 真的老了 試解一下解不出來...
: 1.
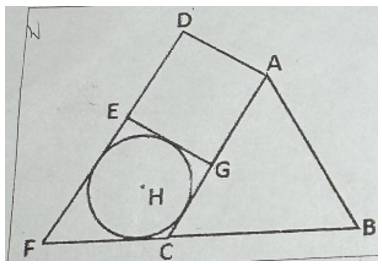
: ABC是正三角形
: ADEG是正方形
: 圓H是內切圓 求AG:GC比值？
: https://i.meee.com.tw/mdT71FU.png
題目乍看條件很多但是最重要的是以下兩點:
1. 圓H的直徑等於ADEG正方形的邊長
2. 角GCF=120度
連HC, 做H到GC的垂足I, H到CF的垂足J, H到EG的垂足K
三角形CHI跟三角形CHJ全等
因此角HCI = 60度
KGIH為正方形, 因此GI=HK=1/2 AG
HCI為30-60-90的直角三角形
因此CI=HI/根號3 = 1/(2根號3) AG
AG:GC = 1: (1/2 + 1/(2根號3)) = 2 : (1+1/根號3)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.224.51.219 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1732154423.A.BEA.html
※ 編輯: mantour (36.224.51.219 臺灣), 11/21/2024 10:00:50
※ 編輯: mantour (36.224.51.219 臺灣), 11/21/2024 10:01:05