Re: [中學] 兩題中學數學 (國三)

[deathcustom (Full House)]

※ 引述《Rimowa (德國品質)》之銘言：
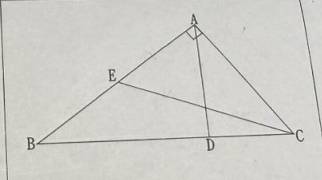
: 1.∠BAC為直角 E為AB中點 ∠AEC=∠BAD CD=7 求BC=?
: https://i.meee.com.tw/56AHezO.png
: 交點應該是外心 不過暫時沒想到往下一步算法
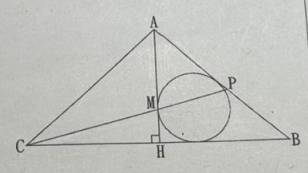
: 2.△ABC是等腰 AB=AC=10 BC=12 AH與BC垂直
: △ABH之內切圓與AH交於M CM交AB於P 求△APC面積？
: https://i.meee.com.tw/OEthuZ3.png
: 初步是把P點往下做垂足到BH上為K
: 然後先求出內切圓半徑2 然後將△APC拆解成AMC跟APM兩個三角形
: AMC面積18 PK可用平行線比例求出 然後算出APM為10 加起來△APC=28
: 但覺得怪怪的 因為P往下做垂足到BH上為K其實未必與圓相切 感覺做法有錯
: 答案也不確定
: 想請教
(1) 圓是三角型ABH的內切圓，所以表示圓心O到A點的連線AO是角BAH的角平分線

(2) 又，角CMB=角AMP，所以角MCB=(角MAP)/2

(3) 由(1)與(2)，線CP正交於線AO

(4) 由(3)，所以三角形AMP被AO分為兩個全等三角型

(5) 由(4)，所以三角形AMO全等於三角型APO

(6) 所以OP正交於AP Q.E.D.

從這邊出發

AH = 8(畢氏定理基本)

MH = r = 8*6/(20+8+6) = 2

AP = AM = 6

這邊就可以接回Honor大的算式後半部

--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 211.23.191.211 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1737368516.A.9CC.html
→ deathcustom : 忽然發現邏輯上有點怪怪的，回家再補
→ musicbox810 : (2)角CMB=角AMP有沒有打錯?
→ musicbox810 : (2) 又，角CM'H'=角AMP，所以角MCB=(角MAP)/2 這段
→ musicbox810 : 是不是假設AMP為等腰三角形? 我覺得應該還要用上題
→ musicbox810 : 目其他的條件
→ deathcustom : 我說邏輯上的錯誤就是因為不小心這樣假設了
→ deathcustom : 但是那是不對的，容我細想