※ 引述《Rimowa (德國品質)》之銘言：
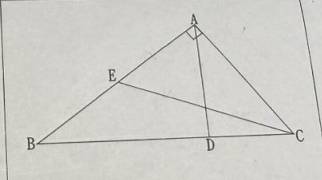
: 1.∠BAC為直角 E為AB中點 ∠AEC=∠BAD CD=7 求BC=?
: https://i.meee.com.tw/56AHezO.png
: 交點應該是外心 不過暫時沒想到往下一步算法
AD 跟 EC 交點為 P
角 AEC = 角 BAD
角DAC = pi/2 - 角BAD = pi/2 - 角AEC = 角ACE
=> PE=PE=PC
=> 三角形APB面積 = 1/2 三角形ABC面積 = 三角形APC面積+三角形APC面積
AE=EB
=> 三角形APC面積 = 三角形BPC面積
=> 三角形APB面積:三角形APC面積:三角形BPC面積=2:1:1
=> BD:DC = 三角形APB面積:三角形APC面積=2:1
=> BC = 21
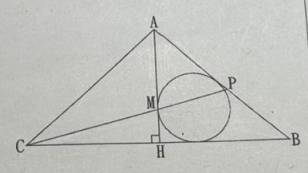
: 2.△ABC是等腰 AB=AC=10 BC=12 AH與BC垂直
: △ABH之內切圓與AH交於M CM交AB於P 求△APC面積？
: https://i.meee.com.tw/OEthuZ3.png
: 初步是把P點往下做垂足到BH上為K
: 然後先求出內切圓半徑2 然後將△APC拆解成AMC跟APM兩個三角形
: AMC面積18 PK可用平行線比例求出 然後算出APM為10 加起來△APC=28
: 但覺得怪怪的 因為P往下做垂足到BH上為K其實未必與圓相切 感覺做法有錯
: 答案也不確定
: 想請教
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.224.29.243 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1737382370.A.C8D.html
※ 編輯: mantour (36.224.29.243 臺灣), 01/20/2025 22:15:19