Re: [中學] 不要太依賴chatgpt

[Honor1984 (奈何上天造化弄人？)]

昨天我有嘗試純粹從座標處理(只看數字1和0)，

剛剛看到有人貼AI的解法，似乎有點雷同，

但是我的作法還是多了一些論證，不是純土法煉鋼硬列舉

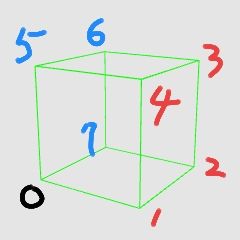
依照正方體空間的點分布，由低到高分別為：

第一層(100)：只有1個1的點集合，共3點

第二層(110)：只有2個1的點集合，共3點

第三層(111)：有3個1的點集合，共1點

高層點與低層點內積 <= 低層點1的個數 => 本題計算出的內積值 <= 2

每層挑2相異點作內積 < 該層點1的個數

由上面兩條自然限制，可以對本題內積值作進一步分類

(1)內積值 = 2：

(111)配(110)：3種，狀況已用完

(2)內積值 = 1：

(111)配(100)：3種

(110)配(110)：3種

(110)配(100)：6種

期望值 = [2*3 + 1(3 + 3 + 6)]/C(7,2) = 18/21 = 6/7

思考邏輯對了，其實剩下來就加法問題

高中排列組合有一大塊是教高中生怎樣有系統的分類和計數

有系統表示有邏輯、不容易錯，

列舉也有分無腦列舉和有想法分類列舉。

就算是無腦列舉，也不是每個人真的都有辦法萬無一失全部列舉得出來

有些沒那麼特殊對稱的情況下還是得用上列舉，

所以不必一味排斥。

像這題直接從空間幾何看可以很簡單判斷最多有哪些內積需要計算，

我是比較偏向從空間下手。

另外，你一值強調P和C，對本題最終結果只差在分子分母約分2!，

你用P增加複本，都除以2!，就會和C一樣，因為本題不允許相同向量對自己內積

固然用P計算好像能幫你避免掉一些前置的分類列舉，

但你還是要扣掉一些狀況不是嗎？

尊重你的作法，

不過根據題意，樣本空間C(7,2)還是一般人比較直接的想法


※ 引述《yueayase (scrya)》之銘言：
: ※ 引述《solumate (尼特學研究者)》之銘言：
: : https://i.mopix.cc/ij7hzM.jpg
: : 看到有人在解這一題，
: : 強調思路是靠自己想出來的，
: : 只是叫chatgpt幫自己寫解題過程。
: : https://i.mopix.cc/xTCpxE.jpg
: : 我看了真的笑死，
: : 連基本計算過程錯誤都沒發現，
: : 擺明了就是看不懂，
: : 在那邊不懂裝懂。
: : 而且錯誤計算卻得到正確答案，
: : 更印證了這個猜測，
: : 根本從頭到尾都靠chatgpt，
: : 然後自己一知半解，
: : 才會鬧出這個大笑話。
: : 甚至他提出的解法思路，
: : 也非常的chatgpt，
: : 一點數學美感都沒有。
: : 明明把內積和拆成XYZ軸，
: : 就只要考慮1或0，
: : 可以很漂亮的把題目解掉，
: : 偏偏要去考慮內積0,1,2三種可能，
: : 結果變成暴力拆解。
: : https://i.mopix.cc/OBvtJ0.jpg
: : 設O為（0,0,0）
: : 考量X軸情況：
: : PQ兩點共有C7取2種可能，
: : 但只有紅色C4取2的情況，
: : X軸內積和才為1，
: : 其餘皆為0
: : 所以X軸期望值為：
: : 1*［C4取2] [C7取2］
: : =2/7
: : 而立方體是三軸對稱，
: : 所以答案就是
: : 2/7+2/7+2/7=6/7
: : 這樣解，
: : 明明就乾淨俐落很多。
: : 只能說數學無捷徑，
: : 還是不要過度依賴chatgpt啊。
: https://chatgpt.com/share/695b957c-ffe8-8008-97fb-d5a6cc3ba798
: 感謝你幫我抓出GPT把計算過程寫錯了
: 好喔，你認為我靠GPT解題作秀，
: 我就附上我叫GPT潤飾的完整過程
: 以及講解給你聽:
: 基本上這題，如果對正立方體座標化
: 很容易可以看出，內積的值決定在P和Q x,y,z分量皆為1的個數
: 如此一來，我可以這樣分析
: (1) 恰1個分量都為1
: 共有C(3,1) * (P(4,2) - C(2,1) *2) = 3 * (12 - 2*2) = 3 * 8 = 24
: 第1個C(3,1)是x,y,z取一個分量
: 接著把剩下2個分量，視為binary string: 00, 01, 10, 11
: 因為P、Q相異，所以我們可以把這4個取出2的相異的(用排列)
: 然後要避開有其中1位同時為1的，這可以從剩下2分量，取1個分量，
: 然後最後一個分量可以有 第一個為0，另一個為1，或第一個為1，另一個為0，共2種
: 舉例: x分量都為1
: P Q (y,z)可以從(0,0) (0,1) (1,0) (1,1)：選2個不同的當作P Q的剩下2個分量
: 像是:
: P(1, 0, 0)
: Q(1, 0, 1)
: 但這要排除像是這樣:
: P(1, 1, 0)
: Q(1, 1, 1)
: 因為這組會讓內積為2
: 但這樣算就等同把
: P(1, 0, 0) Q(1, 0, 1)
: 和
: P(1, 0, 1) Q(1, 0, 0)
: 視為不同的
: 如此一來，樣本空間不應是C(7,2)，而應該是P(7,2)
: (2) 內積為2
: 這反而比Case (1)單純，只需要這樣算: C(3,2) * 2 = 3 * 2 = 6
: 理由:
: 從x,y,z選2個分量，指定他們為1，放進P、Q對應位置
: 因為希望P、Q相異，所以一樣0和1的指定有2種選擇
: 例如:
: (1, 1, 0) => P
: (1, 1, 1) => Q
: (1, 1, 1) => P
: (1, 1, 0) => Q
: (3) 內積為3 => 必須要P、Q都是(1,1,1)，但題目要求取出相異兩點，所以不可能
: 所以期望值就是:
: 24/P(7,2)  * 1 + 6/P(7,2) * 2
: = 24/42 * 1 + 6/42 * 2
: =  4/7 * 1 + 1/7 *2
: = 4/7 + 2/7
: = 6/7
: 答案無誤
: 這也給我們一個教訓:
: 不要相信AI的算術能力
: AI的算術往往會有奇怪的地方
: 還有就是:
: 的確啦，我這種解法還不夠漂亮
: 的確不是最佳解
: 但這應該已經是比較能夠平民化，
: 靠著做一般參考書基本題，想到的快速解法了
: 很多老師教排列組合和機率的時候
: 往往講不清楚: 為什麼這時候樣本空間要用排列? 為什麼這時要用組合? 為什麼都可以?
: 這題就是最好的示範:
: 如果你沒像最佳解那種想法，使用C(7,2)當樣本空間，
: 就會像很多市面上的解答，和網路解題老師的答案
: 要把情況分的很多，少考慮一種就GG了~~~
: 如果因為計算錯誤就認為這個想法錯...
: 其實這也透露出讀者的理解力在哪...
: 說真的，我承認我的文字表達能力不好，
: 所以會用GPT修飾我的文字，希望能簡短好懂一點
: 我那時只檢查他有沒有把我的語意和邏輯弄錯
: 沒有細看GPT算術有沒有寫錯是我的疏失
: 但這解法基本上方向和手段都正確無誤，且不複雜
: 如果有人沒辦法理解，記得去複習高中排列組合和機率吧
: 因為我的過程都是基礎題用到的

--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.224.148.156 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1768116589.A.1B6.html
※ 編輯: Honor1984 (36.224.148.156 臺灣), 01/11/2026 15:38:19
→ yueayase    : 我並非反對列舉或是用這種方式分類
→ yueayase    : 而是發現到很多列舉方式會出現過於複雜的問題
→ yueayase    : 那種分法在腦筋不清楚時，容易錯
→ yueayase    : 雖然您覺得我還是需要在1的時候做減掉的動作
→ yueayase    : 但我認為至少那樣，我頂多只須扣除一種(且容易想)
→ yueayase    : 的狀況，所以我認為這樣反而比較好思考
→ yueayase    : 我作法扣掉的狀況也只有一種 所以我強調P和C
→ yueayase    : 並非是要證明我的方法好棒棒，而是想強調:
→ yueayase    : 有時不一定要照直覺的樣本空間選取，反而有機會變
→ yueayase    : 簡單一點
→ yueayase    : 當然我會認為我的做法比較好，有個前提:
→ yueayase    : 我是用機率*報酬的期望值計算思考，所以認為能
→ yueayase    : 轉化成我想要的這種算法，我那樣弄比較簡單
→ yueayase    : 你們很多人都是基於內積的加總/C(7,2)
→ yueayase    : 基於總獎金/總次數，我必須承認 你們的方法比較好
→ yueayase    : 但對於用機率*報酬開始想的，用C(7,2)大多情況會
→ yueayase    : 變的像大多數解答那樣比較醜
推 yueayase    : 真要我說: 我想強調的是不要每次都先入為主覺得
→ yueayase    : 應該用C或P 這樣有些題目會有些狀況
→ yueayase    : 應該根據列舉的大致組態，以及方法的可行性和效率
→ yueayase    : 再決定用哪一個
→ mantour     : 這題用P或C的差別應該沒有大到顯然用哪個才是對的
→ mantour     : ，每個人切入角度不同，算出來答案對，思路也解釋
→ mantour     : 到別人看得懂就好了。
→ mantour     : 不過如果是考試有部分給分，不小心算錯一步結果最
→ mantour     : 後答案錯的時候，跟參考解答用相同的思路，有可能
→ mantour     : 拿到比較多分XD
→ mantour     : 研究出來用P還是C最好的時間，可能隨便先想到哪一
→ mantour     : 個就開始算都算出來了
→ yueayase    : 是的，其實當學生時代很難有很多間研究完整
→ yueayase    : 真的是憑感覺的部分多了點，現在不用考試
→ yueayase    : 反而有辦法把過去不了解的地方理解透徹