作者ACGfans (ACGfans)
看板puzzle
標題[問題] 計算次方
時間Sun Dec 29 19:02:29 2019
假如我們要計算 n 的 15 次方
我們可以很簡單的列出以下式子
(1) n^1 * n^1 = n^2
(2) n^2 * n^1 = n^3
...
(14) n^14 * n^1 = n^15
經過 14 次計算後得到
我們也可以有比較聰明的作法
(1) n^1 * n^1 = n^2
(2) n^2 * n^2 = n^4
(3) n^4 * n^4 = n^8
(4) n^8 * n^4 = n^12
(5) n^12 * n^2 = n^14
(6) n^14 * n^1 = n^15
經過 6 次計算後得到
不過我們可以有更聰明的方法
(1) n^1 * n^1 = n^2
(2) n^2 * n^1 = n^3
(3) n^3 * n^3 = n^6
(4) n^6 * n^6 = n^12
(5) n^12 * n^3 = n^15
經過 5 次計算即可得到
請問: 假如我們要計算 n 的 77 次方
最少需要幾次計算? 作法為何?
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 125.231.73.128 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/puzzle/M.1577617352.A.655.html
※ 編輯: ACGfans (125.231.73.128 臺灣), 12/29/2019 19:09:51
→ buffalobill: 1,2,4,5,9,18,36,41,77 12/29 20:36
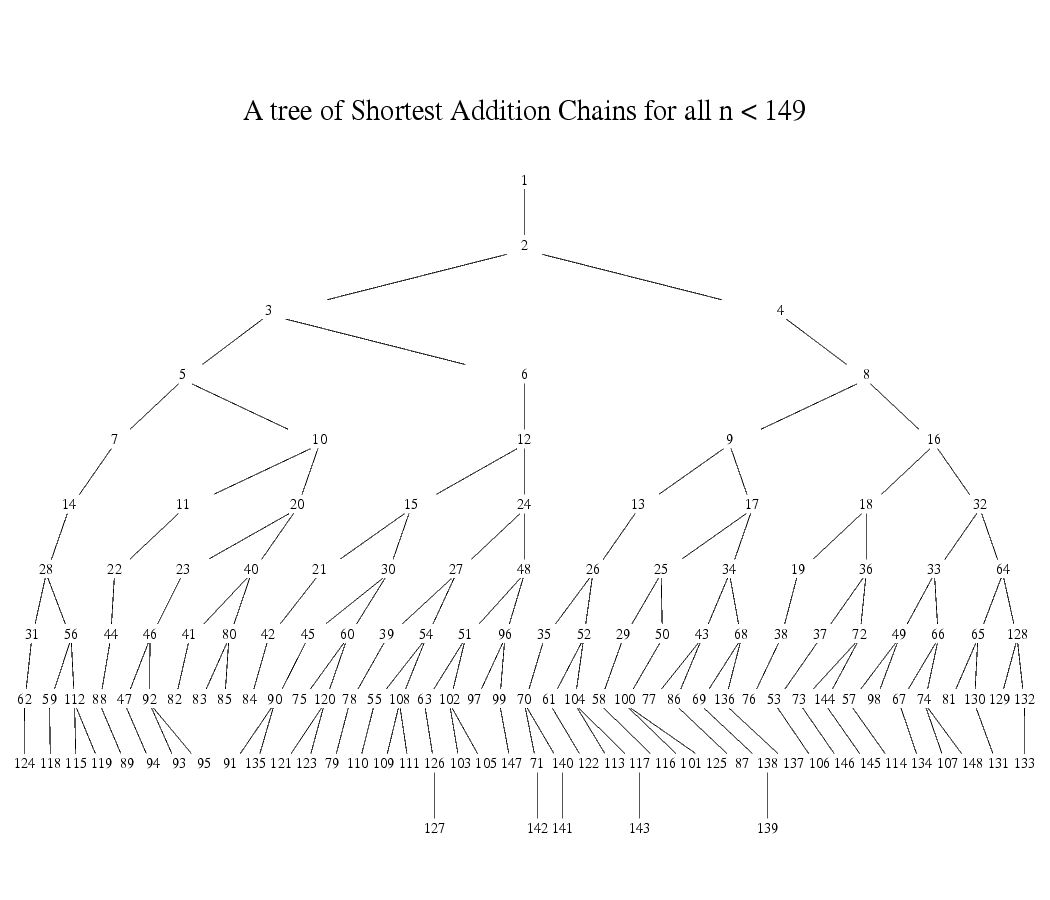
→ ACGfans: 八次正解 有興趣的可以去查查看加法鏈 addition chains 12/30 19:39